Journey to the IO Monad (Part 3.1)

In this second final post about the IO monad, i like to share with you my experience in modelling concurrent data structures using cats-effect. In my experience, given any programming language with concurrency intrinsics (e.g. mutexes , locks, semaphores in C++, Java, Haskell) you should be able to model any concurrent data structure.

The context of the exercise i did was to start by asking myself the question :

“IO monad in cats-effect looks a lot like Haskell’s IO monad, if i have some familiarity with the latter can i possibly reproduce some structures and is this universal? “ . I’m happy to say that the answer is Yes on the first part of the question and Maybe on the latter where universality applicability is still under investigation.

Concurrency is a hard topic to learn and even harder to master, so let’s start by looking at something small ; understand what it does, how it does what it says its doing and see how we can replicate the behaviour. By small, i mean the ADT should be simple and uses at most 1 concurrent primitive like lock, mutexes, semaphore.

The example i’m going to use is a buffered channel (credit: Concurrent Haskell paper) and we shall see how we can build a channel with unbounded buffering; the idea is that we start by having a reader & writer which initially points to the same cell; as the channel progresses with more incoming data the writer’s end would be referring to the latest datum dropped while the reader’s end would be focusing on the last read datum.

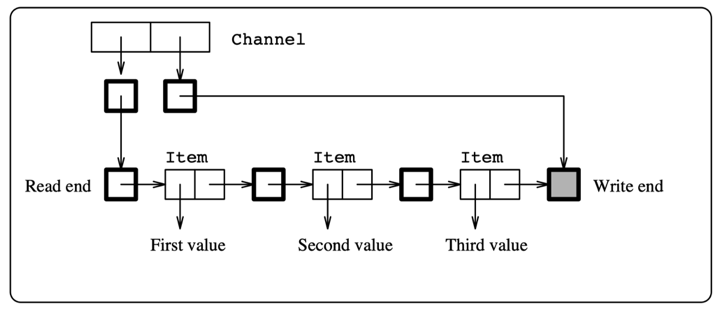
Below is a schematic of how a channel with 3 items would look like (assuming nothing has been read): Unbounded Buffer

A channel with unbounded buffering (implemented with MVars) To model this, we must first describe it. I know that this channel should allow multiple and concurrent tasks (i.e. threads , processes) to be able to read and write from it and the data type is described below:

type Stream[A, F[_]] = MVar[F, Item[A,F]]
case class Item[A,F[_]](head : A, tail : Stream[A,F])
case class Channel[A, F[_]:Concurrent](
  reader : MVar[F, Stream[A,F]],        // Reader
  writer : MVar[F, Stream[A,F]]         // Writer
)

First, Stream is a ADT which captures the notion of a queue of items that is either empty or contains an Item. The MVars in the implementation is necessary so that read and write operations can modify the reader and writer of the channel respectively.

Therefore, you can imagine the Stream to be a list which consists of alternating Items and fullMVars terminated with a “hole” which is an empty MVar.

Second, let’s look at how the newChannel ,readChannel and writeChannel implementation looks like. Creating a new channel is a matter of creating 3 holes (reader, writer & stream itself) and populating into the Channel ADT; reading from the channel is by consuming the reader’s end while replacing it with the remaining of the list and lastly for writing to such a channel involves creating a new empty Stream to become the new hole, extracting the old hole and replacing it with the new hole and then putting the Item into the old hole. The polymorphic implementations are shown below (click here to see the full source code):

def newChannel[A,F[_]:Concurrent] : F[Channel[A,F]] =
  for {
    r <- MVar.uncancelableEmpty[F, Item[A,F]]
    a <- MVar.uncancelableOf[F, Stream[A,F]](r)
    b <- MVar.uncancelableOf[F, Stream[A,F]](r)
  } yield Channel(a, b)
def readChannel[A, F[_]:Concurrent](ch: Channel[A,F]) : F[A] =
  for {
    stream <- ch.reader.take
    item   <- stream.read
    _      <- ch.reader.put(item.tail)
  } yield item.head
def writeChannel[A, F[_]:Concurrent](ch: Channel[A,F], value: A) : F[Unit] =
  for {
    newHole <- MVar.empty[F, Item[A,F]]
    oldHole <- ch.writer.take
    _ <- ch.writer.put(newHole)
    _ <- oldHole.put(Item(value, newHole))
  } yield ()

At this point in time, i’ve just described the core operations of this unbounded channel and quite naturally i need to see that it works. Time to test it out! The testing should carry the consideration that

MVar implementation in cats-effect is correct ;
IO implementation is correct and this is important because the IO monad should still work the same if i were to replace it with ZIO’s IO.

Below is an example of creating a channel which carries integers and 4 values are put into the channel concurrently (via Fibers) and reading the channel where the reading order would be depended on the writing order; a different sequence of values would be read on each run.

**Note **: if you comment the “.start” for the 4 Fibers, you should see the sequence (1,2,3,4) printed every time.

def putNDrain =
  for {
    channel <- newChannel[Int, IO] // using the cats-effect IO
    a  <- writeChannel(channel, 1).start // Fiber 1
    b  <- writeChannel(channel, 2).start // Fiber 2
    c  <- writeChannel(channel, 3).start // Fiber 3
    d  <- writeChannel(channel, 4).start // Fiber 4
    el1 <- readChannel(channel)
    el2 <- readChannel(channel) 
    el3 <- readChannel(channel)
    el4 <- readChannel(channel)
  } yield (el1, el2, el3, el4) // uncomment the ".start" to see sequential evaluation.
println(putNDrain.unsafeRunSync) // run it.

You can see how useful the IO monad (in cats-effect) really is because i have just described a polymorphic approach to creating a concurrent data structure, then we described a series of operations to use the channel (the sequencing of computations is guaranteed by the IO monad); and finally it is demonstrated to work.

Next, let’s add the capability to sum all the integers of this channel. The idea is to similar to folding the list (i.e. catamorphism) and adding the value seen to the last known accumulated value till we reach the end of the list and return the accumulated value. The continuation function in this recursion is another IO action (or monad) and is evaluated lazily till we reached the end. The idea is demonstrated below and click here for the source code:

def sumChannel[F[_]:Concurrent](ch: Channel[Int,F], sum: Long) : F[Long] = {
  val F = implicitly[Concurrent[F]]
  for {
    flag   <- ch.reader.read
    empty  <- flag.isEmpty
    result <- if (empty) F.pure(sum) else
      F.suspend {
        for {
          stream <- ch.reader.take
          item   <- stream.read
          _      <- ch.reader.put(item.tail)
          sum    <- sumChannel(ch, sum+item.head.toLong)
        } yield sum
      }
    } yield result  
  } // end of "sumChannel"

Summing this channel depends on where the reader’s end is and in this scenario i have deliberately not read anything which means it pointing to the start of the channel. Given this assumption, it should be correct regardless of the order of the writes and to see if its true i ran 2 scenarios:

populate the channel with 9 values sequentially
repeat item (a) but have concurrent writes instead and below is the version of scenario (b):

// Concurrent writes with no interfering reads, summing at the end.
def sumTask =
  for {
    channel <- newChannel[Int,IO]
    _ <- writeChannel(channel, 1).start
    _ <- writeChannel(channel, 2).start
    _ <- writeChannel(channel, 3).start
    _ <- writeChannel(channel, 4).start
    _ <- writeChannel(channel, 5).start
    _ <- writeChannel(channel, 6).start
    _ <- writeChannel(channel, 7).start
    _ <- writeChannel(channel, 8).start
    _ <- writeChannel(channel, 9).start
    sum <- sumChannel(channel, 0L)
  } yield sum
sumTask.unsafeRunSync // return 45

Here’s a trickier scenario where there are interfering reads between the concurrent writes, and i’m curious as to whether the algorithm still works. Turns out it still does ☺ . Here’s what it looks like:

def sumTask2 =
  for {
    channel <- newChannel[Int,IO]
    _ <- writeChannel(channel, 1).start
    _ <- writeChannel(channel, 2).start
    _ <- writeChannel(channel, 3).start
    _ <- writeChannel(channel, 4).start
    _ <- readChannel(channel) *> 
         readChannel(channel) *> 
         readChannel(channel)          // reader points to "4".
    _ <- writeChannel(channel, 5).start
    _ <- writeChannel(channel, 6).start
    _ <- readChannel(channel) *> 
         readChannel(channel) *> 
         readChannel(channel)          // reader points to start.
    _ <- writeChannel(channel, 7).start
    _ <- writeChannel(channel, 8).start
    _ <- writeChannel(channel, 9).start
    sum <- sumChannel(channel, 0L)
  } yield sum
sumTask2.unsafeRunSync // returns 24, can you see why?

Link to other related posts: